11 Algorithms library [algorithms]
11.5 Sorting and related operations [alg.sorting]
All the operations in [alg.sorting] take an optional binary callable predicate of type Comp that defaults to less<>.
Comp is a callable object ( ISO/IEC 14882:2014 §[func.require]). The return value of the invoke operation applied to an object of type Comp, when contextually converted to bool (Clause ISO/IEC 14882:2014 §[conv]), yields true if the first argument of the call is less than the second, and false otherwise. Comp comp is used throughout for algorithms assuming an ordering relation. It is assumed that comp will not apply any non-constant function through the dereferenced iterator.
A sequence is sorted with respect to a comparator and projection comp and proj if for every iterator i pointing to the sequence and every non-negative integer n such that i + n is a valid iterator pointing to an element of the sequence, invoke(comp, invoke(proj, *(i + n)), invoke(proj, *i)) == false.
A sequence [start,finish) is partitioned with respect to an expression f(e) if there exists an integer n such that for all 0 <= i < distance(start, finish), f(*(start + i)) is true if and only if i < n.
In the descriptions of the functions that deal with ordering relationships we frequently use a notion of equivalence to describe concepts such as stability. The equivalence to which we refer is not necessarily an operator==, but an equivalence relation induced by the strict weak ordering. That is, two elements a and b are considered equivalent if and only if !(a < b) && !(b < a).
11.5.1 Sorting [alg.sort]
11.5.1.1 sort [sort]
template <RandomAccessIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
I sort(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <RandomAccessRange Rng, class Comp = less<>, class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
safe_iterator_t<Rng>
sort(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Effects: Sorts the elements in the range [first,last).
Returns: last.
Complexity: Ο(Nlog(N)) (where N == last - first) comparisons, and twice as many applications of the projection.
11.5.1.2 stable_sort [stable.sort]
template <RandomAccessIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
I stable_sort(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <RandomAccessRange Rng, class Comp = less<>, class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
safe_iterator_t<Rng>
stable_sort(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Effects: Sorts the elements in the range [first,last).
Returns: last.
Complexity: Let N == last - first. If enough extra memory is available, N log(N) comparisons. Otherwise, at most N log2(N) comparisons. In either case, twice as many applications of the projection as the number of comparisons.
Remarks: Stable ( ISO/IEC 14882:2014 §[algorithm.stable]).
11.5.1.3 partial_sort [partial.sort]
template <RandomAccessIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
I partial_sort(I first, I middle, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <RandomAccessRange Rng, class Comp = less<>, class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
safe_iterator_t<Rng>
partial_sort(Rng&& rng, iterator_t<Rng> middle, Comp comp = Comp{},
Proj proj = Proj{});
Returns: last.
Complexity: It takes approximately (last - first) * log(middle - first) comparisons, and exactly twice as many applications of the projection.
11.5.1.4 partial_sort_copy [partial.sort.copy]
template <InputIterator I1, Sentinel<I1> S1, RandomAccessIterator I2, Sentinel<I2> S2,
class Comp = less<>, class Proj1 = identity, class Proj2 = identity>
requires IndirectlyCopyable<I1, I2> && Sortable<I2, Comp, Proj2> &&
IndirectStrictWeakOrder<Comp, projected<I1, Proj1>, projected<I2, Proj2>>
I2
partial_sort_copy(I1 first, S1 last, I2 result_first, S2 result_last,
Comp comp = Comp{}, Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
template <InputRange Rng1, RandomAccessRange Rng2, class Comp = less<>,
class Proj1 = identity, class Proj2 = identity>
requires IndirectlyCopyable<iterator_t<Rng1>, iterator_t<Rng2>> &&
Sortable<iterator_t<Rng2>, Comp, Proj2> &&
IndirectStrictWeakOrder<Comp, projected<iterator_t<Rng1>, Proj1>,
projected<iterator_t<Rng2>, Proj2>>
safe_iterator_t<Rng2>
partial_sort_copy(Rng1&& rng, Rng2&& result_rng, Comp comp = Comp{},
Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
Effects: Places the first min(last - first, result_last - result_first) sorted elements into the range [result_first,result_first + min(last - first, result_last - result_first)).
Returns: The smaller of: result_last or result_first + (last - first).
Complexity: Approximately
(last - first) * log(min(last - first, result_last - result_first))
comparisons, and exactly twice as many applications of the projection.
11.5.1.5 is_sorted [is.sorted]
template <ForwardIterator I, Sentinel<I> S, class Proj = identity,
IndirectStrictWeakOrder<projected<I, Proj>> Comp = less<>>
bool is_sorted(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <ForwardRange Rng, class Proj = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng>, Proj>> Comp = less<>>
bool
is_sorted(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Returns: is_sorted_until(first, last, comp, proj) == last
template <ForwardIterator I, Sentinel<I> S, class Proj = identity,
IndirectStrictWeakOrder<projected<I, Proj>> Comp = less<>>
I is_sorted_until(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <ForwardRange Rng, class Proj = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng>, Proj>> Comp = less<>>
safe_iterator_t<Rng>
is_sorted_until(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Returns: If distance(first, last) < 2, returns last. Otherwise, returns the last iterator i in [first,last] for which the range [first,i) is sorted.
Complexity: Linear.
11.5.2 Nth element [alg.nth.element]
template <RandomAccessIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
I nth_element(I first, I nth, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <RandomAccessRange Rng, class Comp = less<>, class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
safe_iterator_t<Rng>
nth_element(Rng&& rng, iterator_t<Rng> nth, Comp comp = Comp{}, Proj proj = Proj{});
After nth_element the element in the position pointed to by nth is the element that would be in that position if the whole range were sorted, unless nth == last. Also for every iterator i in the range [first,nth) and every iterator j in the range [nth,last) it holds that: invoke(comp, invoke(proj, *j), invoke(proj, *i)) == false.
Returns: last.
Complexity: Linear on average.
11.5.3 Binary search [alg.binary.search]
All of the algorithms in this section are versions of binary search and assume that the sequence being searched is partitioned with respect to an expression formed by binding the search key to an argument of the comparison function and projection. They work on non-random access iterators minimizing the number of comparisons, which will be logarithmic for all types of iterators. They are especially appropriate for random access iterators, because these algorithms do a logarithmic number of steps through the data structure. For non-random access iterators they execute a linear number of steps.
11.5.3.1 lower_bound [lower.bound]
template <ForwardIterator I, Sentinel<I> S, class T, class Proj = identity,
IndirectStrictWeakOrder<const T*, projected<I, Proj>> Comp = less<>>
I
lower_bound(I first, S last, const T& value, Comp comp = Comp{},
Proj proj = Proj{});
template <ForwardRange Rng, class T, class Proj = identity,
IndirectStrictWeakOrder<const T*, projected<iterator_t<Rng>, Proj>> Comp = less<>>
safe_iterator_t<Rng>
lower_bound(Rng&& rng, const T& value, Comp comp = Comp{}, Proj proj = Proj{});
Requires: The elements e of [first,last) shall be partitioned with respect to the expression invoke(comp, invoke(proj, e), value).
Returns: The furthermost iterator i in the range [first,last] such that for every iterator j in the range [first,i) the following corresponding condition holds: invoke(comp, invoke(proj, *j), value) != false.
Complexity: At most log2(last - first) + Ο(1) applications of the comparison function and projection.
11.5.3.2 upper_bound [upper.bound]
template <ForwardIterator I, Sentinel<I> S, class T, class Proj = identity,
IndirectStrictWeakOrder<const T*, projected<I, Proj>> Comp = less<>>
I
upper_bound(I first, S last, const T& value, Comp comp = Comp{}, Proj proj = Proj{});
template <ForwardRange Rng, class T, class Proj = identity,
IndirectStrictWeakOrder<const T*, projected<iterator_t<Rng>, Proj>> Comp = less<>>
safe_iterator_t<Rng>
upper_bound(Rng&& rng, const T& value, Comp comp = Comp{}, Proj proj = Proj{});
Requires: The elements e of [first,last) shall be partitioned with respect to the expression !invoke(comp, value, invoke(proj, e)).
Returns: The furthermost iterator i in the range [first,last] such that for every iterator j in the range [first,i) the following corresponding condition holds: invoke(comp, value, invoke(proj, *j)) == false.
Complexity: At most log2(last - first) + Ο(1) applications of the comparison function and projection.
11.5.3.3 equal_range [equal.range]
template <ForwardIterator I, Sentinel<I> S, class T, class Proj = identity,
IndirectStrictWeakOrder<const T*, projected<I, Proj>> Comp = less<>>
tagged_pair<tag::begin(I), tag::end(I)>
equal_range(I first, S last, const T& value, Comp comp = Comp{}, Proj proj = Proj{});
template <ForwardRange Rng, class T, class Proj = identity,
IndirectStrictWeakOrder<const T*, projected<iterator_t<Rng>, Proj>> Comp = less<>>
tagged_pair<tag::begin(safe_iterator_t<Rng>),
tag::end(safe_iterator_t<Rng>)>
equal_range(Rng&& rng, const T& value, Comp comp = Comp{}, Proj proj = Proj{});
Requires:
The elements
e
of
[first,last)
shall be partitioned with respect to the expressions
invoke(comp, invoke(proj, e), value)
and
!invoke(comp, value, invoke(proj, e)).
Also, for all elements
e
of
[first, last),
invoke(comp, invoke(proj, e), value)
shall imply
!invoke(comp, value, invoke(proj, e)).
Returns:
Complexity: At most 2 * log2(last - first) + Ο(1) applications of the comparison function and projection.
11.5.3.4 binary_search [binary.search]
template <ForwardIterator I, Sentinel<I> S, class T, class Proj = identity,
IndirectStrictWeakOrder<const T*, projected<I, Proj>> Comp = less<>>
bool
binary_search(I first, S last, const T& value, Comp comp = Comp{},
Proj proj = Proj{});
template <ForwardRange Rng, class T, class Proj = identity,
IndirectStrictWeakOrder<const T*, projected<iterator_t<Rng>, Proj>> Comp = less<>>
bool
binary_search(Rng&& rng, const T& value, Comp comp = Comp{},
Proj proj = Proj{});
Requires: The elements e of [first,last) are partitioned with respect to the expressions invoke(comp, invoke(proj, e), value) and !invoke(comp, value, invoke(proj, e)). Also, for all elements e of [first, last), invoke(comp, invoke(proj, e), value) shall imply !invoke(comp, value, invoke(proj, e)).
Returns: true if there is an iterator i in the range [first,last) that satisfies the corresponding conditions: invoke(comp, invoke(proj, *i), value) == false && invoke(comp, value, invoke(proj, *i)) == false.
Complexity: At most log2(last - first) + Ο(1) applications of the comparison function and projection.
11.5.4 Merge [alg.merge]
template <InputIterator I1, Sentinel<I1> S1, InputIterator I2, Sentinel<I2> S2,
WeaklyIncrementable O, class Comp = less<>, class Proj1 = identity,
class Proj2 = identity>
requires Mergeable<I1, I2, O, Comp, Proj1, Proj2>
tagged_tuple<tag::in1(I1), tag::in2(I2), tag::out(O)>
merge(I1 first1, S1 last1, I2 first2, S2 last2, O result,
Comp comp = Comp{}, Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
template <InputRange Rng1, InputRange Rng2, WeaklyIncrementable O, class Comp = less<>,
class Proj1 = identity, class Proj2 = identity>
requires Mergeable<iterator_t<Rng1>, iterator_t<Rng2>, O, Comp, Proj1, Proj2>
tagged_tuple<tag::in1(safe_iterator_t<Rng1>),
tag::in2(safe_iterator_t<Rng2>),
tag::out(O)>
merge(Rng1&& rng1, Rng2&& rng2, O result,
Comp comp = Comp{}, Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
Effects: Copies all the elements of the two ranges [first1,last1) and [first2,last2) into the range [result,result_last), where result_last is result + (last1 - first1) + (last2 - first2). If an element a precedes b in an input range, a is copied into the output range before b. If e1 is an element of [first1,last1) and e2 of [first2,last2), e2 is copied into the output range before e1 if and only if bool(invoke(comp, invoke(proj2, e2), invoke(proj1, e1))) is true.
Requires: The ranges [first1,last1) and [first2,last2) shall be sorted with respect to comp, proj1, and proj2. The resulting range shall not overlap with either of the original ranges.
Returns: make_tagged_tuple<tag::in1, tag::in2, tag::out>(last1, last2, result_last).
Complexity: At most (last1 - first1) + (last2 - first2) - 1 applications of the comparison function and each projection.
Remarks: Stable ( ISO/IEC 14882:2014 §[algorithm.stable]).
template <BidirectionalIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
I
inplace_merge(I first, I middle, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <BidirectionalRange Rng, class Comp = less<>, class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
safe_iterator_t<Rng>
inplace_merge(Rng&& rng, iterator_t<Rng> middle, Comp comp = Comp{},
Proj proj = Proj{});
Effects: Merges two sorted consecutive ranges [first,middle) and [middle,last), putting the result of the merge into the range [first,last). The resulting range will be in non-decreasing order; that is, for every iterator i in [first,last) other than first, the condition invoke(comp, invoke(proj, *i), invoke(proj, *(i - 1))) will be false.
Requires: The ranges [first,middle) and [middle,last) shall be sorted with respect to comp and proj.
Returns: last
Complexity: When enough additional memory is available, (last - first) - 1 applications of the comparison function and projection. If no additional memory is available, an algorithm with complexity N log(N) (where N is equal to last - first) may be used.
Remarks: Stable ( ISO/IEC 14882:2014 §[algorithm.stable]).
11.5.5 Set operations on sorted structures [alg.set.operations]
This section defines all the basic set operations on sorted structures. They also work with multisets ( ISO/IEC 14882:2014 §[multiset]) containing multiple copies of equivalent elements. The semantics of the set operations are generalized to multisets in a standard way by defining set_union() to contain the maximum number of occurrences of every element, set_intersection() to contain the minimum, and so on.
11.5.5.1 includes [includes]
template <InputIterator I1, Sentinel<I1> S1, InputIterator I2, Sentinel<I2> S2,
class Proj1 = identity, class Proj2 = identity,
IndirectStrictWeakOrder<projected<I1, Proj1>, projected<I2, Proj2>> Comp = less<>>
bool
includes(I1 first1, S1 last1, I2 first2, S2 last2, Comp comp = Comp{},
Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
template <InputRange Rng1, InputRange Rng2, class Proj1 = identity,
class Proj2 = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng1>, Proj1>,
projected<iterator_t<Rng2>, Proj2>> Comp = less<>>
bool
includes(Rng1&& rng1, Rng2&& rng2, Comp comp = Comp{},
Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
Returns: true if [first2,last2) is empty or if every element in the range [first2,last2) is contained in the range [first1,last1). Returns false otherwise.
Complexity: At most 2 * ((last1 - first1) + (last2 - first2)) - 1 applications of the comparison function and projections.
11.5.5.2 set_union [set.union]
template <InputIterator I1, Sentinel<I1> S1, InputIterator I2, Sentinel<I2> S2,
WeaklyIncrementable O, class Comp = less<>, class Proj1 = identity, class Proj2 = identity>
requires Mergeable<I1, I2, O, Comp, Proj1, Proj2>
tagged_tuple<tag::in1(I1), tag::in2(I2), tag::out(O)>
set_union(I1 first1, S1 last1, I2 first2, S2 last2, O result, Comp comp = Comp{},
Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
template <InputRange Rng1, InputRange Rng2, WeaklyIncrementable O,
class Comp = less<>, class Proj1 = identity, class Proj2 = identity>
requires Mergeable<iterator_t<Rng1>, iterator_t<Rng2>, O, Comp, Proj1, Proj2>
tagged_tuple<tag::in1(safe_iterator_t<Rng1>),
tag::in2(safe_iterator_t<Rng2>),
tag::out(O)>
set_union(Rng1&& rng1, Rng2&& rng2, O result, Comp comp = Comp{},
Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
Effects: Constructs a sorted union of the elements from the two ranges; that is, the set of elements that are present in one or both of the ranges.
Requires: The resulting range shall not overlap with either of the original ranges.
Returns:
make_tagged_tuple<tag::in1, tag::in2, tag::out>(last1, last2, result + n),
where n is
the number of elements in the constructed range.
Complexity: At most 2 * ((last1 - first1) + (last2 - first2)) - 1 applications of the comparison function and projections.
Remarks: If [first1,last1) contains m elements that are equivalent to each other and [first2,last2) contains n elements that are equivalent to them, then all m elements from the first range shall be copied to the output range, in order, and then max(n - m, 0) elements from the second range shall be copied to the output range, in order.
11.5.5.3 set_intersection [set.intersection]
template <InputIterator I1, Sentinel<I1> S1, InputIterator I2, Sentinel<I2> S2,
WeaklyIncrementable O, class Comp = less<>, class Proj1 = identity, class Proj2 = identity>
requires Mergeable<I1, I2, O, Comp, Proj1, Proj2>
O
set_intersection(I1 first1, S1 last1, I2 first2, S2 last2, O result,
Comp comp = Comp{}, Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
template <InputRange Rng1, InputRange Rng2, WeaklyIncrementable O,
class Comp = less<>, class Proj1 = identity, class Proj2 = identity>
requires Mergeable<iterator_t<Rng1>, iterator_t<Rng2>, O, Comp, Proj1, Proj2>
O
set_intersection(Rng1&& rng1, Rng2&& rng2, O result,
Comp comp = Comp{}, Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
Effects: Constructs a sorted intersection of the elements from the two ranges; that is, the set of elements that are present in both of the ranges.
Requires: The resulting range shall not overlap with either of the original ranges.
Returns: The end of the constructed range.
Complexity: At most 2 * ((last1 - first1) + (last2 - first2)) - 1 applications of the comparison function and projections.
Remarks: If [first1,last1) contains m elements that are equivalent to each other and [first2,last2) contains n elements that are equivalent to them, the first min(m, n) elements shall be copied from the first range to the output range, in order.
11.5.5.4 set_difference [set.difference]
template <InputIterator I1, Sentinel<I1> S1, InputIterator I2, Sentinel<I2> S2,
WeaklyIncrementable O, class Comp = less<>, class Proj1 = identity, class Proj2 = identity>
requires Mergeable<I1, I2, O, Comp, Proj1, Proj2>
tagged_pair<tag::in1(I1), tag::out(O)>
set_difference(I1 first1, S1 last1, I2 first2, S2 last2, O result,
Comp comp = Comp{}, Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
template <InputRange Rng1, InputRange Rng2, WeaklyIncrementable O,
class Comp = less<>, class Proj1 = identity, class Proj2 = identity>
requires Mergeable<iterator_t<Rng1>, iterator_t<Rng2>, O, Comp, Proj1, Proj2>
tagged_pair<tag::in1(safe_iterator_t<Rng1>), tag::out(O)>
set_difference(Rng1&& rng1, Rng2&& rng2, O result,
Comp comp = Comp{}, Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
Effects: Copies the elements of the range [first1,last1) which are not present in the range [first2,last2) to the range beginning at result. The elements in the constructed range are sorted.
Requires: The resulting range shall not overlap with either of the original ranges.
Returns: {last1, result + n}, where n is the number of elements in the constructed range.
Complexity: At most 2 * ((last1 - first1) + (last2 - first2)) - 1 applications of the comparison function and projections.
Remarks: If [first1,last1) contains m elements that are equivalent to each other and [first2,last2) contains n elements that are equivalent to them, the last max(m - n, 0) elements from [first1,last1) shall be copied to the output range.
11.5.5.5 set_symmetric_difference [set.symmetric.difference]
template <InputIterator I1, Sentinel<I1> S1, InputIterator I2, Sentinel<I2> S2,
WeaklyIncrementable O, class Comp = less<>, class Proj1 = identity, class Proj2 = identity>
requires Mergeable<I1, I2, O, Comp, Proj1, Proj2>
tagged_tuple<tag::in1(I1), tag::in2(I2), tag::out(O)>
set_symmetric_difference(I1 first1, S1 last1, I2 first2, S2 last2, O result,
Comp comp = Comp{}, Proj1 proj1 = Proj1{},
Proj2 proj2 = Proj2{});
template <InputRange Rng1, InputRange Rng2, WeaklyIncrementable O,
class Comp = less<>, class Proj1 = identity, class Proj2 = identity>
requires Mergeable<iterator_t<Rng1>, iterator_t<Rng2>, O, Comp, Proj1, Proj2>
tagged_tuple<tag::in1(safe_iterator_t<Rng1>),
tag::in2(safe_iterator_t<Rng2>),
tag::out(O)>
set_symmetric_difference(Rng1&& rng1, Rng2&& rng2, O result, Comp comp = Comp{},
Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
Effects: Copies the elements of the range [first1,last1) that are not present in the range [first2,last2), and the elements of the range [first2,last2) that are not present in the range [first1,last1) to the range beginning at result. The elements in the constructed range are sorted.
Requires: The resulting range shall not overlap with either of the original ranges.
Returns:
make_tagged_tuple<tag::in1, tag::in2, tag::out>(last1, last2, result + n),
where n is
the number of elements in the constructed range.
Complexity: At most 2 * ((last1 - first1) + (last2 - first2)) - 1 applications of the comparison function and projections.
Remarks: If [first1,last1) contains m elements that are equivalent to each other and [first2,last2) contains n elements that are equivalent to them, then |m - n| of those elements shall be copied to the output range: the last m - n of these elements from [first1,last1) if m > n, and the last n - m of these elements from [first2,last2) if m < n.
11.5.6 Heap operations [alg.heap.operations]
A heap is a particular organization of elements in a range between two random access iterators [a,b). Its two key properties are:
There is no element greater than *a in the range and
*a may be removed by pop_heap(), or a new element added by push_heap(), in Ο(log(N)) time.
These properties make heaps useful as priority queues.
make_heap() converts a range into a heap and sort_heap() turns a heap into a sorted sequence.
11.5.6.1 push_heap [push.heap]
template <RandomAccessIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
I push_heap(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <RandomAccessRange Rng, class Comp = less<>, class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
safe_iterator_t<Rng>
push_heap(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Effects: Places the value in the location last - 1 into the resulting heap [first,last).
Requires: The range [first,last - 1) shall be a valid heap.
Returns: last
Complexity: At most log(last - first) applications of the comparison function and projection.
11.5.6.2 pop_heap [pop.heap]
template <RandomAccessIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
I pop_heap(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <RandomAccessRange Rng, class Comp = less<>, class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
safe_iterator_t<Rng>
pop_heap(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Requires: The range [first,last) shall be a valid non-empty heap.
Effects: Swaps the value in the location first with the value in the location last - 1 and makes [first,last - 1) into a heap.
Returns: last
Complexity: At most 2 * log(last - first) applications of the comparison function and projection.
11.5.6.3 make_heap [make.heap]
template <RandomAccessIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
I make_heap(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <RandomAccessRange Rng, class Comp = less<>, class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
safe_iterator_t<Rng>
make_heap(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Effects: Constructs a heap out of the range [first,last).
Returns: last
Complexity: At most 3 * (last - first) applications of the comparison function and projection.
11.5.6.4 sort_heap [sort.heap]
template <RandomAccessIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
I sort_heap(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <RandomAccessRange Rng, class Comp = less<>, class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
safe_iterator_t<Rng>
sort_heap(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Effects: Sorts elements in the heap [first,last).
Requires: The range [first,last) shall be a valid heap.
Returns: last
Complexity: At most N log(N) comparisons (where N == last - first), and exactly twice as many applications of the projection.
11.5.6.5 is_heap [is.heap]
template <RandomAccessIterator I, Sentinel<I> S, class Proj = identity,
IndirectStrictWeakOrder<projected<I, Proj>> Comp = less<>>
bool is_heap(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <RandomAccessRange Rng, class Proj = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng>, Proj>> Comp = less<>>
bool
is_heap(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Returns: is_heap_until(first, last, comp, proj) == last
template <RandomAccessIterator I, Sentinel<I> S, class Proj = identity,
IndirectStrictWeakOrder<projected<I, Proj>> Comp = less<>>
I is_heap_until(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <RandomAccessRange Rng, class Proj = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng>, Proj>> Comp = less<>>
safe_iterator_t<Rng>
is_heap_until(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Returns: If distance(first, last) < 2, returns last. Otherwise, returns the last iterator i in [first,last] for which the range [first,i) is a heap.
Complexity: Linear.
11.5.7 Minimum and maximum [alg.min.max]
template <class T, class Proj = identity,
IndirectStrictWeakOrder<projected<const T*, Proj>> Comp = less<>>
constexpr const T& min(const T& a, const T& b, Comp comp = Comp{}, Proj proj = Proj{});
Returns: The smaller value.
Remarks: Returns the first argument when the arguments are equivalent.
template <Copyable T, class Proj = identity,
IndirectStrictWeakOrder<projected<const T*, Proj>> Comp = less<>>
constexpr T min(initializer_list<T> rng, Comp comp = Comp{}, Proj proj = Proj{});
template <InputRange Rng, class Proj = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng>, Proj>> Comp = less<>>
requires Copyable<value_type_t<iterator_t<Rng>>>
value_type_t<iterator_t<Rng>>
min(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Requires: distance(rng) > 0.
Returns: The smallest value in the initializer_list or range.
Remarks: Returns a copy of the leftmost argument when several arguments are equivalent to the smallest.
template <class T, class Proj = identity,
IndirectStrictWeakOrder<projected<const T*, Proj>> Comp = less<>>
constexpr const T& max(const T& a, const T& b, Comp comp = Comp{}, Proj proj = Proj{});
Returns: The larger value.
Remarks: Returns the first argument when the arguments are equivalent.
template <Copyable T, class Proj = identity,
IndirectStrictWeakOrder<projected<const T*, Proj>> Comp = less<>>
constexpr T max(initializer_list<T> rng, Comp comp = Comp{}, Proj proj = Proj{});
template <InputRange Rng, class Proj = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng>, Proj>> Comp = less<>>
requires Copyable<value_type_t<iterator_t<Rng>>>
value_type_t<iterator_t<Rng>>
max(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Requires: distance(rng) > 0.
Returns: The largest value in the initializer_list or range.
Remarks: Returns a copy of the leftmost argument when several arguments are equivalent to the largest.
template <class T, class Proj = identity,
IndirectStrictWeakOrder<projected<const T*, Proj>> Comp = less<>>
constexpr tagged_pair<tag::min(const T&), tag::max(const T&)>
minmax(const T& a, const T& b, Comp comp = Comp{}, Proj proj = Proj{});
Returns: {b, a} if b is smaller than a, and {a, b} otherwise.
Remarks: Returns {a, b} when the arguments are equivalent.
Complexity: Exactly one comparison and exactly two applications of the projection.
template <Copyable T, class Proj = identity,
IndirectStrictWeakOrder<projected<const T*, Proj>> Comp = less<>>
constexpr tagged_pair<tag::min(T), tag::max(T)>
minmax(initializer_list<T> rng, Comp comp = Comp{}, Proj proj = Proj{});
template <InputRange Rng, class Proj = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng>, Proj> Comp = less<>>
requires Copyable<value_type_t<iterator_t<Rng>>>
tagged_pair<tag::min(value_type_t<iterator_t<Rng>>),
tag::max(value_type_t<iterator_t<Rng>>)>
minmax(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Requires: distance(rng) > 0.
Returns: {x, y}, where x has the smallest and y has the largest value in the initializer_list or range.
Remarks: x is a copy of the leftmost argument when several arguments are equivalent to the smallest. y is a copy of the rightmost argument when several arguments are equivalent to the largest.
Complexity: At most (3/2) * distance(rng) applications of the corresponding predicate, and at most twice as many applications of the projection.
template <ForwardIterator I, Sentinel<I> S, class Proj = identity,
IndirectStrictWeakOrder<projected<I, Proj>> Comp = less<>>
I min_element(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <ForwardRange Rng, class Proj = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng>, Proj>> Comp = less<>>
safe_iterator_t<Rng>
min_element(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Returns:
The first iterator
i
in the range
[first,last)
such that for every iterator
j
in the range
[first,last)
the following corresponding condition holds:
invoke(comp, invoke(proj, *j), invoke(proj, *i)) == false.
Returns
last
if
first == last.
Complexity: Exactly max((last - first) - 1, 0) applications of the comparison function and exactly twice as many applications of the projection.
template <ForwardIterator I, Sentinel<I> S, class Proj = identity,
IndirectStrictWeakOrder<projected<I, Proj>> Comp = less<>>
I max_element(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <ForwardRange Rng, class Proj = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng>, Proj>> Comp = less<>>
safe_iterator_t<Rng>
max_element(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Returns:
The first iterator
i
in the range
[first,last)
such that for every iterator
j
in the range
[first,last)
the following corresponding condition holds:
invoke(comp, invoke(proj, *i), invoke(proj, *j)) == false.
Returns
last
if
first == last.
Complexity: Exactly max((last - first) - 1, 0) applications of the comparison function and exactly twice as many applications of the projection.
template <ForwardIterator I, Sentinel<I> S, class Proj = identity,
IndirectStrictWeakOrder<projected<I, Proj>> Comp = less<>>
tagged_pair<tag::min(I), tag::max(I)>
minmax_element(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <ForwardRange Rng, class Proj = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng>, Proj>> Comp = less<>>
tagged_pair<tag::min(safe_iterator_t<Rng>),
tag::max(safe_iterator_t<Rng>)>
minmax_element(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Returns: {first, first} if [first,last) is empty, otherwise {m, M}, where m is the first iterator in [first,last) such that no iterator in the range refers to a smaller element, and where M is the last iterator in [first,last) such that no iterator in the range refers to a larger element.
Complexity:
At most
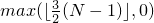 applications of the comparison function and
at most twice as many applications of the projection,
where N is distance(first, last).
applications of the comparison function and
at most twice as many applications of the projection,
where N is distance(first, last).
11.5.8 Lexicographical comparison [alg.lex.comparison]
template <InputIterator I1, Sentinel<I1> S1, InputIterator I2, Sentinel<I2> S2,
class Proj1 = identity, class Proj2 = identity,
IndirectStrictWeakOrder<projected<I1, Proj1>, projected<I2, Proj2>> Comp = less<>>
bool
lexicographical_compare(I1 first1, S1 last1, I2 first2, S2 last2,
Comp comp = Comp{}, Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
template <InputRange Rng1, InputRange Rng2, class Proj1 = identity,
class Proj2 = identity,
IndirectStrictWeakOrder<projected<iterator_t<Rng1>, Proj1>,
projected<iterator_t<Rng2>, Proj2>> Comp = less<>>
bool
lexicographical_compare(Rng1&& rng1, Rng2&& rng2, Comp comp = Comp{},
Proj1 proj1 = Proj1{}, Proj2 proj2 = Proj2{});
Returns: true if the sequence of elements defined by the range [first1,last1) is lexicographically less than the sequence of elements defined by the range [first2,last2) and false otherwise.
Complexity: At most 2*min((last1 - first1), (last2 - first2)) applications of the corresponding comparison and projections.
Remarks: If two sequences have the same number of elements and their corresponding elements are equivalent, then neither sequence is lexicographically less than the other. If one sequence is a prefix of the other, then the shorter sequence is lexicographically less than the longer sequence. Otherwise, the lexicographical comparison of the sequences yields the same result as the comparison of the first corresponding pair of elements that are not equivalent.
for ( ; first1 != last1 && first2 != last2 ; ++first1, (void) ++first2) {
if (invoke(comp, invoke(proj1, *first1), invoke(proj2, *first2))) return true;
if (invoke(comp, invoke(proj2, *first2), invoke(proj1, *first1))) return false;
}
return first1 == last1 && first2 != last2;
Remarks: An empty sequence is lexicographically less than any non-empty sequence, but not less than any empty sequence.
11.5.9 Permutation generators [alg.permutation.generators]
template <BidirectionalIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
bool next_permutation(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <BidirectionalRange Rng, class Comp = less<>,
class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
bool
next_permutation(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Effects: Takes a sequence defined by the range [first,last) and transforms it into the next permutation. The next permutation is found by assuming that the set of all permutations is lexicographically sorted with respect to comp and proj. If such a permutation exists, it returns true. Otherwise, it transforms the sequence into the smallest permutation, that is, the ascendingly sorted one, and returns false.
Complexity: At most (last - first)/2 swaps.
template <BidirectionalIterator I, Sentinel<I> S, class Comp = less<>,
class Proj = identity>
requires Sortable<I, Comp, Proj>
bool prev_permutation(I first, S last, Comp comp = Comp{}, Proj proj = Proj{});
template <BidirectionalRange Rng, class Comp = less<>,
class Proj = identity>
requires Sortable<iterator_t<Rng>, Comp, Proj>
bool
prev_permutation(Rng&& rng, Comp comp = Comp{}, Proj proj = Proj{});
Effects: Takes a sequence defined by the range [first,last) and transforms it into the previous permutation. The previous permutation is found by assuming that the set of all permutations is lexicographically sorted with respect to comp and proj.
Returns: true if such a permutation exists. Otherwise, it transforms the sequence into the largest permutation, that is, the descendingly sorted one, and returns false.
Complexity: At most (last - first)/2 swaps.